Simple Statistics Problem
Consider the NCAA Basketball Tournament, an event which is happening right now. The tournament features 64 teams in four divisions of 16 teams. In the first round, the team with #1 seed plays the #16 team. #2 plays #15, and so on. To date, a #16 seed has never beaten a #1 seed. A quick search on Sports Reference reveals this is accurate.
So, the question for all you predictive analytics masters out there. Given that this event has never happened, what is the probability that a #16 seed will upset a #1 seed?
Philosophically, Not Zero Percent
This event has never happened but it is certainly plausible. In fact, I'd be wary to even call it a "black swan" -- out of 116 games, #15 has upset #2 a total of 7 times. According to some data collected by Roto Guru you'll see the following breakdowns per seed (out of 116 games):
Team1_Seed Team2_Seed Team1_Wins Team1_Wins_Percent
1 16 116 100%
2 15 109 94%
3 14 99 85%
4 13 91 78%
5 12 75 65%
6 11 77 66%
7 10 70 60%
8 9 56 48%
If you were just to take the proportions and make those your probability of wins, you'd get zero. Intuitively, this is nonsense. So what do we do?
A Generalized Approach: Bayes
So I'm going to steal a technique from a http://www.databozo.com/ and generalize for a second. Take the bayesian fair coin question -- if we flip a coin and get 1,2,3,4,5... heads in a row, what does the distribution of bayesian posteriors look like (given we bucket hypotheses into 1,2,3...100)? Well, we can do this and we get something like the below:
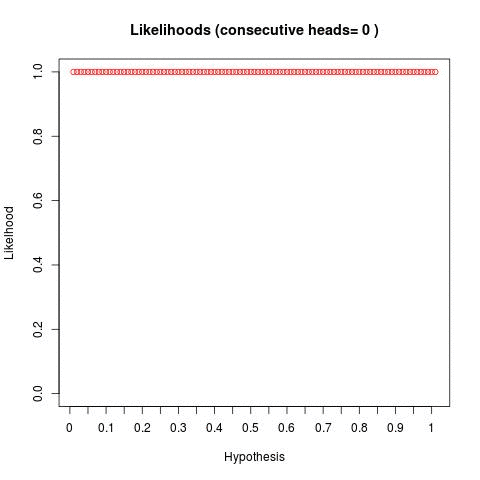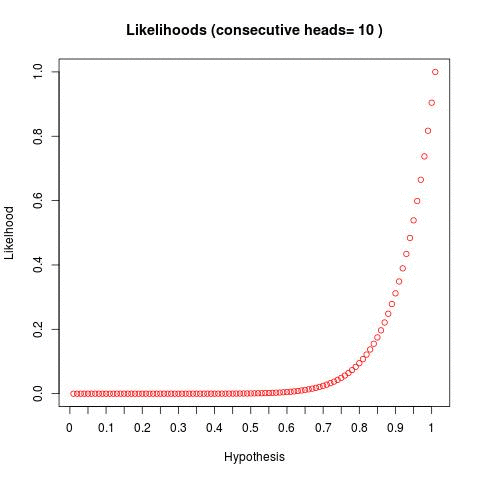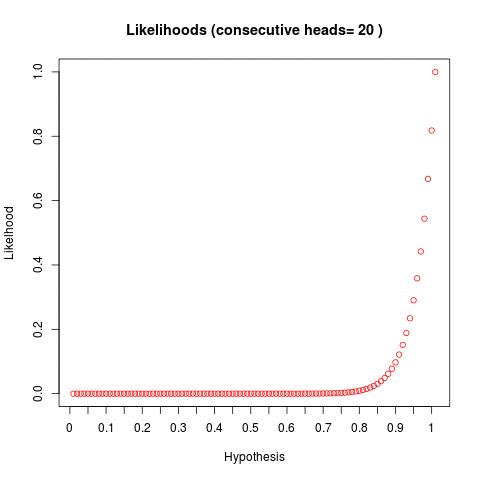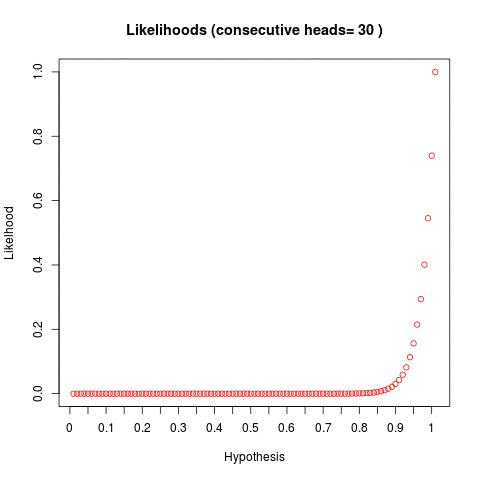
We can see - as we flip a coin and continually get a result of heads - our "distribution" of hypotheses skew to the right. This tells us - as we flip more coins and get more heads, the hypotheses to the right become statistically more likely.
But what about if we flipped a coin and got heads 116 times? In this case, the likelihood of it being a 99% weighted heads coin is 0.03 and the likelihood of it being a 100% weighted heads coin is 1 (because we've seen NO counter evidence). The likelihood of it being an even coin is very very small (1.155434e-36). In this distribution, 95% of the density is in 0-98% and the rest is in the 99%-100% bucket.
If we map this back to the NCAA game example, this means that we can claim that with 95% confidence, the #16 team has between an approximately 0-1% chance of winning.
Another colleague of mine, Drew Fustin pointed me to a famous physics paper (Feldman and Cousins) on this topic, which seems to use a similar and more complex bayesian method that gives a range of 0-2.63% chance of #16 winning (assuming a known mean background). I like their approach, it is the best treatment I could find on this topic.
Yet, I Still Struggle
So, I still struggle with this philosophically. Here's why: I can flip a coin and observe a heads and observe a tails. But, with a #16 v #1 upset, we've never observed this. We're using an abstraction (coin flipping) to model a non-abstract outcome. I realize that every scientific model is precisely this -- but something makes me philosophically uncomfortable about this. This is a notion I'm still exploring philosophically (maybe a future blog update). It's lead me to question the notion of "predictive analytics", something I have been a zealot for.
In addition, this type of prediction: predicting an event where we have no observations is something that happens in business and politics every single day. From climate research, to government predictions, to economists -- they're making confident predictions about complex outcomes that we've never observed. Even with our toy example above, it's totally plausible that the #16 team has a 2% chance of winning. Unless we're really careful with examining errors, we will probably have the tendency to under-estimate these never-before-seen things. We should be treating every never-before-seen event like physicists treat neutrino detection!
Full Disclosure: I've also been reading Taleb's book Antifragile. The book covers randomness and Black Swan events, the synthesis of these ideas in my head.